Le triangle de Pascal (1623-1662) est un tableau de nombres qui permet de déterminer, par une relation de récurrence, les coefficients binomiaux \( \binom{p}{n} \)
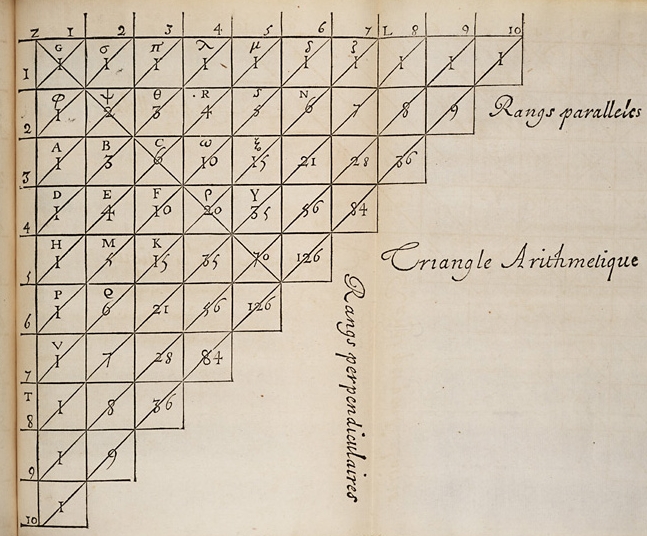
Nous verrons dans ce chapitre qu'il n'est pas toujours aisé de réussir à "compter" des éléments dans des ensembles... En effet, il faut se demander si par exemple "On peut prendre des élemetns plusieurs fois ?", si 'l'ordre a une importane ?", etc
Le Rubik’s Cube compte 43 252 003 274 489 856 000 configurations différentes dans sa version la plus célèbre (faces constituées de neuf cubes). En supposant qu’un humain puisse tester une combinaison chaque seconde, il lui faudrait donc plus de 1 371 512 027 000 années pour toutes les rencontrer, soit environ 300 fois l’âge de la Terre.
| Diapo | Cours |
|---|---|
| Diapo | Cours |
| Formule du triangle de Pascal |
|---|
| Ne pas confondre combinaison et arrangement |
|---|