

Le logarithme népérien en hommage au mathématicien écossais John Napier est à l'origine des premières tables logarithmiques. Celles-ci ne furent cependant pas des tables de logarithmes népériens.
On date en général la naissance des logarithmes népériens de 1647, date à laquelle Grégoire de Saint-Vincent travaille sur la quadrature de l'hyperbole et démontre que la fonction obtenue vérifie la propriété des fonctions logarithmes (transformation d'un produit en somme).
La fonction ln s'est d'ailleurs appelée un certain temps fonction logarithme hyperbolique compte tenu de sa découverte comme aire sous l'hyperbole. Le terme de logarithme naturel (En mathématiques le logarithme naturel ou logarithme népérien, est le logarithme de base e....) apparaît pour la première fois dans une note de Nicolaus Mercator en 1668, quand celui-ci met en place sa série de Mercator. Sa série exploitée par Newton (méthode des fluxions et des suites infinies 1671), permet de calculer assez simplement les valeurs du logarithme de Grégoire de Saint-Vincent. Le calcul des autres logarithmes apparaît alors bien compliqué. Le logarithme de Grégoire de Saint-Vincent devient alors le logarithme le plus "simple" et le plus naturel.
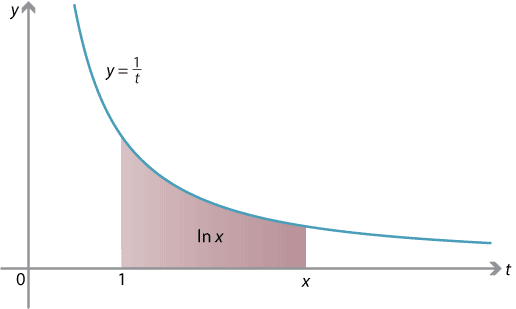
Formellement, ln(x) peut être défini comme l'aire du domaine délimité par la courbe représentative de la fonction \( x\mapsto \frac{1}{x} \), l'axe des abscisses et les droites d'abscisses 1 et x.
Cette approche, respectueuse de la réalité historique, permet de prouver l'existence de la fonction ln et ses diverses propriétés qu'on vera dans ce chapitre
| Diapo | Cours |
|---|---|
| Diapo | Cours |
| Démonstration : \( \ln (a \times b) = \ln a + \ln b \) |
|---|
| Transformation d'écriture | Dérivée de \( x \mapsto \ln x \) |
|---|---|
| Etude complète de fonction | Tangente et fonction \( \ln x \) | Vrai ou Faux : \( \ln x \) |
|---|---|---|